第一章  函数、极阻与连续考核知识点

本章考试的重点是：函数的定义；基本初等函数；极限概念与极限运算；无穷小的比较；连续概念与初等函数的连续性。

福建专升本高等数学考试的考点繁杂，题型多变，为了帮助同学们更好的学习数学，根据高等数学考试大纲的要求，聚英专升本的小编总结了福建专升本高等数学第一章函数、极阻与连续考核知识点常见考点：

一、一元函数的定义

一元函数是指函数方程式中只包含一个自变量。例如y=F(x)。与一元函数对应的为多元函数，顾名思义函数方程中包含多个自变量。

定义域：使函数()yfx有意义的自变量的全体，即自变量x的取值范围D

二、函数的表示法（包括分段表示法）

（1）公式法：用数学表达式表示函数的方法 

（2）分段函数：当自变量在定义域内的不同区间取值时，用不同的表达式表示的函数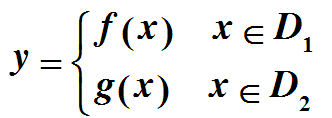 

例如：绝对值函数         

符号函数

取整函数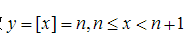

（3）列表法：将一系列自变量x的数值与对应的函数值y列成表格表示函数的方法 

（4）图形法：用图形表示函数的方法

三、函数的简单性——有界性、单调性、奇偶性、周期性

（1）有界性

函数f(x)的定义域为D，f（x）集合D上有定义。

如果存在数K1，使得 f(x)≤K1对任意x∈D都成立，则称函数f(x)在X上有上界。

反之，如果存在数字K2，使得 f(x)≥K2对任意x∈D都成立，则称函数f(x)在D上有下界，而K2称为函数f(x)在D上的一个下界。

如果存在正数M，使得 |f(x)|≤M 对任意x∈D都成立，则称函数在X上有界。如果这样的M不存在，就称函数f(x)在X上无界；等价于，无论对于任何正数M，总存在x1属于X，使得|f(x1)|>M，那么函数f(x)在X上无界。

此外，函数f(x)在X上有界的充分必要条件是它在X上既有上界也有下界。

（2）单调性 

说明：讨论函数的单调性必须指明所在的区间。 

（3）奇偶性

性质：奇函数与偶函数的定义域必定关于原点对称。偶函数的图象关于y轴对称，奇函数的图象关于原点对称.

（4）周期性

对于函数y=f（x），假如存在一个非零常数T，使得当x取定义域内的任何值时，f（x+T）=f（x）都成立，那么就把函数y=f（x）叫做周期函数，不为零的常数T叫做这个函数的周期。

最小正周期:周期函数的周期由无数个，其中正周期中最小的周期为最小正周期 说明：通常所说的函数的周期，指的是最小正周期，但有些周期函数无最小正周期

四.反函数及其图形

五.复合函数

是任何两个函数都可以复合成一个复合函数，只有当Mx∩Du≠Ø时，二者才可以构成一个复合函数。

设函数y=f(u[1]  ）的定义域为Du，值域为Mu，函数u=g(x）的定义域为Dx，值域为Mx，如果Mx∩Du≠Ø，那么对于Mx∩Du内的任意一个x经过u；有唯一确定的y值与之对应，则变量x与y之间通过变量u形成的一种函数关系，这种函数称为复合函数(composite function)，记为：y=f[g(x)]，其中x称为自变量，u为中间变量，y为因变量（即函数）。

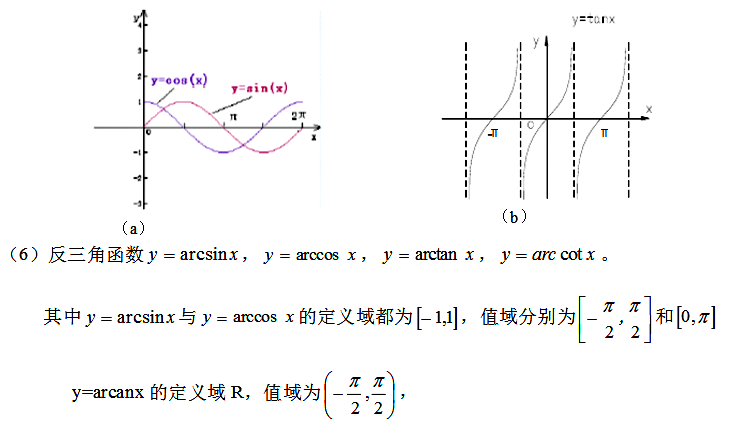
六、基本初等函数与初等函数（包括它们的定义、定义区间、简单性态和图形）

1、基本初等函数

（1）常数函数y=c（c为常数），其图形为一条平行或重合于x轴的直线. 

（2）幂函数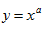（a为实数）,其在第一象限内的图形

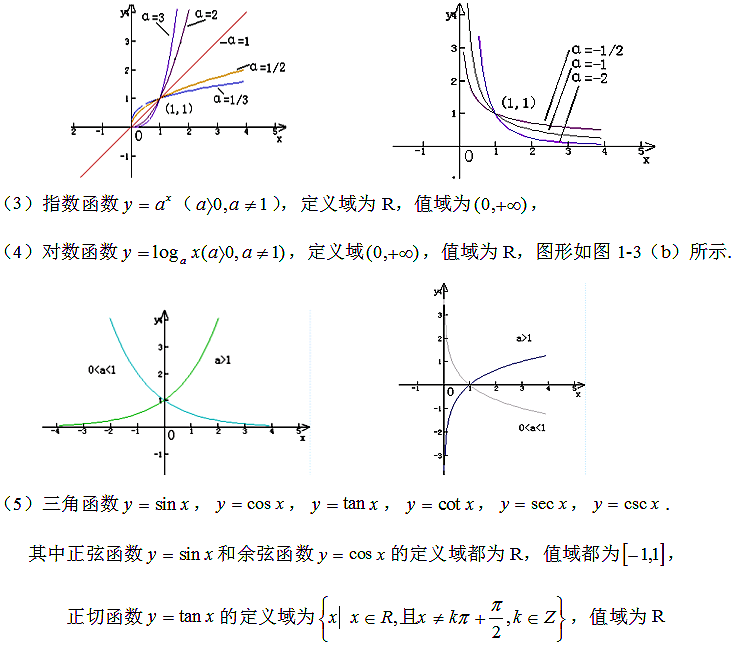
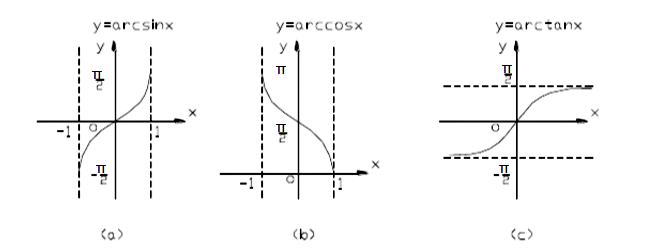
2.初等函数

（1）定义：由基本初等函数经过有限次四则运算和有限次的复合，且可用一个解析式表示的函数，称为初等函数. 

（2）说明：分段函数中有些是初等函数，有些是非初等函数. 

七、数列概念

数列（sequence of number）是以正整数集（或它的有限子集）为定义域的函数，是一列有序的数。数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1项（通常也叫做首项），排在第二位的数称为这个数列的第2项……排在第n位的数称为这个数列的第n项，通常用an表示。

八、数列的极限

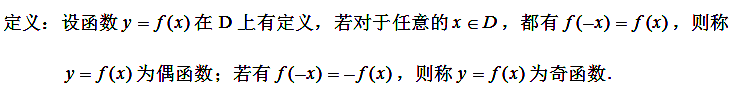
九、收敛数列的性质——有界性、唯一性

① 有界性：收敛数列一定有界。即有界是收敛的必要条件，无界数列一定发散

② 唯一性：收敛数列的极限是唯一的 

十、数列极限的存在准则——单调有界准则

单调有界准则：单调有界数列必有极限

十一、函数的极限（包括当和时，函数极限的定义及左、右极限的定义）

十二、函数极限的存在

十三、函数极限的存在准则——夹逼准则

十四、极限的四则运算法则（包括数列极限与函数极限）

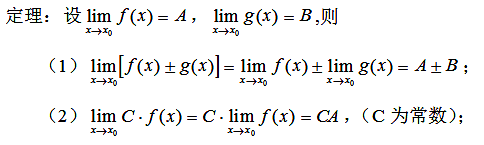
十五、两个重要极限

1.重要极限

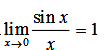
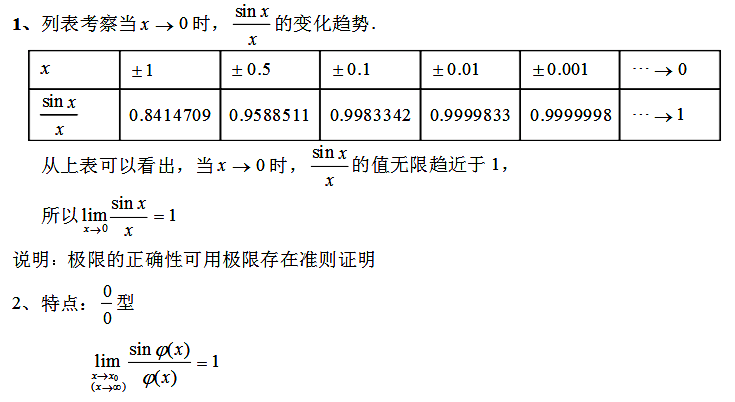
2.重要极限

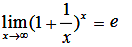
以上就是聚英专升本小编为大家整理的福建专升本高等数学第一章函数、极阻与连续考核知识点，希望能够为同学们的备考提供更清晰的复习思路，祝大家取得好成绩！