第二章 导数与微分

本章考试的重点是：导数的定义及其几何意义；导数作为变化率的概念；可导函数的和、差、积、商的求导运算法则；复合函数求导法则；初等函数的求导问题；微分定义。

福建专升本高等数学考试的考点繁杂，题型多变，为了帮助同学们更好的学习数学，根据高等数学考试大纲的要求，聚英专升本的小编总结了福建专升本高等数学第一章函数、极阻与连续考核知识点常见考点：

一、导数的定义

设函数y=f(x)在点x0的某个领域内有定义，当自变量x在x0处有增量Δx，(x0+Δx)也在该邻域内时，相应地函数取得增量Δy=f(x0+Δx)-f(x0)；如果Δy与Δx之比当Δx→0时极限存在，则称函数y=f(x)在点x0处可导，并称这个极限为函数y=f(x)在点x0处的导数记作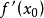 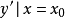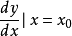； ； ， 即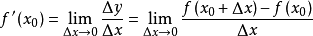

需要指出的是：

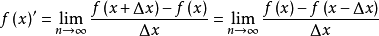两者在数学上是等价的

二、导数的几何意义

三、导数作为函数对自变量的变化率的概念

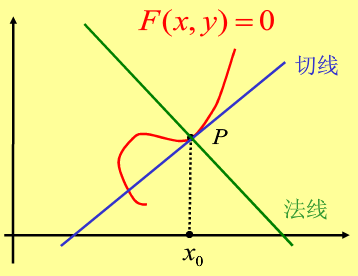
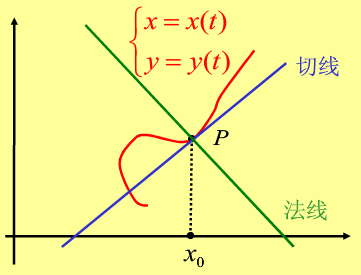
四、平面曲线的切线与法线

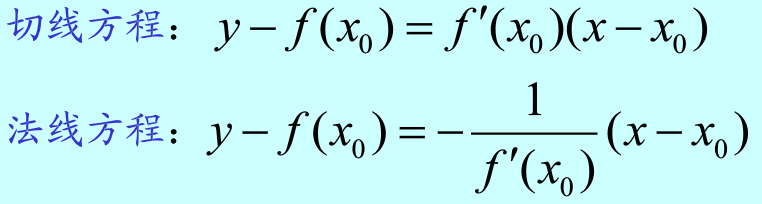
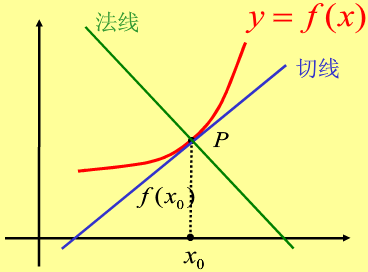
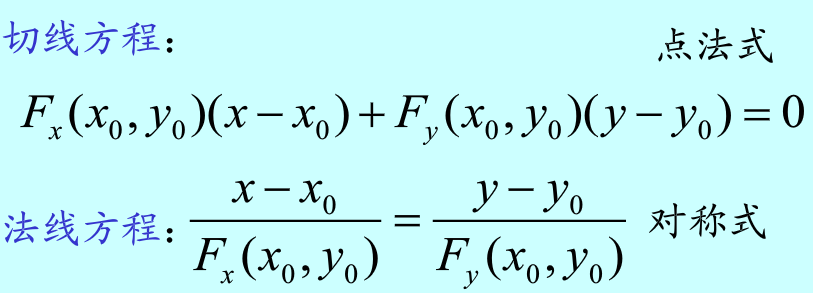
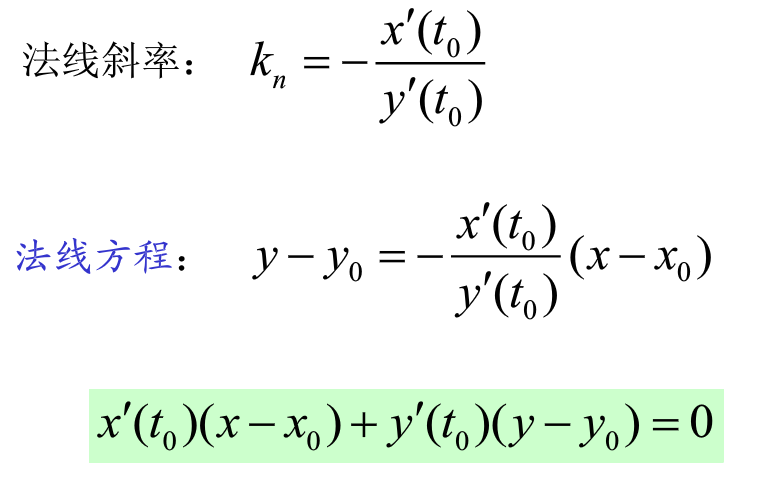
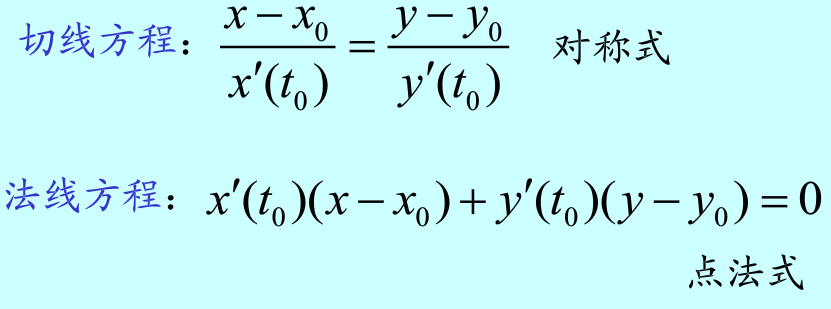
五、函数可导与连续的关系

六、可导函数的和、差、积、商的求导运算法则

七、复合函数的求导法则

八、反函数的求导法则

九、基本初等函数的求导公式及初等函数的求导问题

十、高阶导数

十一、隐函数求导和取对数求导法

十二、由参数方程所确定的函数的求导法

十三、微分的定义

十四、微分的基本公式、运算法则和一阶微分形式不变法